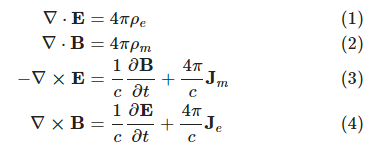Maxwell's equations

Maxwell's equations are differential equations that state the relationships between electric and magnetic fields, and that underlie the wave nature of light. Equation (1) and (2) are Gauss' laws, (3) Faraday's law, (4) Ampere's.

The four equations were originally formulated based on observation. Equation 3, for example, comes from Faraday's law. It relates the rate at which magnetic field is changing, [math]\frac{\partial\mathbf{B}}{\partial t}[/math] to circular flow of electric current, [math]\nabla\boldsymbol{\times}\mathbf{E}[/math].

Maxwell's genius was in completing the four equations and bringing them together, and from the combination seeing that light was an electromagnetic phenomenon. In particular, the speed at which light travels can be deduced from the equations.

Prerequisities

The maths of these equations will make no sense to you whatsoever without the following foundations:

• Understanding of Simple harmonic motion. The key idea is that differential equations relating position, velocity and acceleration can lead to a solution that oscillates.
• Familiarity with vectors in 3 dimensions, Vector product and Cross product. The mathematical operations allow you to calculate the angle between vectors or to take two vectors and find another that is perpendicular to both.
• The Div Grad and Curl differential operations in 3D that are shown here, and in particular why [math]\nabla\cdot(\nabla\times\mathbf{B}) = 0[/math]

No Magnetic Monopoles

To-Be-Written.