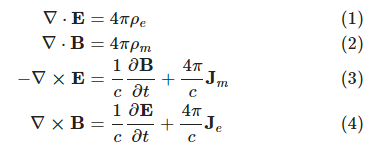Maxwell's equations

Maxwell's equations are partial differential equations that state the relationships between electric and magnetic fields. They underlie the wave nature of light. Equation (1) and (2) are Gauss' laws, (3) Faraday's law of induction, (4) Ampere's circuital law.

The history of how the equations came about is actually helpful in understanding them. Originally the equations were separate observations. Pass a magnet through a coil and you get an electric current. Pass an electric current through a coil, get a magnetic field.

• Equations (1) and (2) in essence state that electric and magnetic fields spread outwards. The lines of force of a magnetic field don't suddenly stop (except at the North or South pole of a magnet). Similarly for an electric field.
• Equation (3), Faraday's law, relates the rate at which magnetic field is changing, [math]\frac{\partial\mathbf{B}}{\partial t}[/math] to circulation of electric field, [math]\nabla\boldsymbol{\times}\mathbf{E}[/math].
• Equation (4), Ampere's law, relates the rate at which electric field is changing, [math]\frac{\partial\mathbf{E}}{\partial t}[/math] to circulation of magnetic field, [math]\nabla\boldsymbol{\times}\mathbf{B}[/math].

Maxwell's genius was in completing the four equations and from the combination conjecturing that light and radio waves were electromagnetic phenomenon. In particular, the speed at which light travels can be deduced from the equations.

It is astonishing that formulae originally created for quantifying relationships between electricity and magnetism led on to an understanding of light and radio transmission, and that both are electromagnetic waves. In the formulae above, the speed of light [math]c[/math] is explicit. In the original arrangement of the equations and using the units of measurement in use at that time, [math]c[/math] was a little more hidden, derived from two quantities called 'permissivity' and 'permitivity'.

Prerequisities

The maths of these equations will make no sense to you whatsoever without the following foundations:

• Understanding of Simple harmonic motion. The key idea is that differential equations relating position, velocity and acceleration can lead to a solution that oscillates.
• Familiarity with vectors in 3 dimensions, Vector product and Cross product. The vector product allows you to calculate the angle between two vectors. The cross product, given two vectors, finds another vector that is perpendicular to both.
• The Div Grad and Curl differential operations in 3D that are shown here, and in particular why [math]\nabla\cdot(\nabla\times\mathbf{B}) = 0[/math]. Div, Grad and Curl are differential operations in 3D space. Maxwell's 3rd and 4th equation relate the results of a spatial derivative of one field (magnetic or electric) with a temporal derivative of the other kind of field.

No Magnetic Monopoles

To-Be-Written.

Integral Version

You can view the differential equations as answering the question 'what happens at each point in space?' and the integral equations as answering 'what happens in each volume of space?'.

Same Equations - Using Integrals

The equivalence of the integral and differential forms of the equations follows from Stoke's Theorem and Green's Theorem. The four differential equations are equivalent to these four integral equations. If you differentiate these integral equations, you get the differential ones. [math] \begin{align} {\oint}\!\!\!\!{\oint}_{\scriptstyle\partial \Omega } & \mathbf{E}\cdot\mathrm{d}\mathbf{S} = 4 \pi \iiint_\Omega \rho_e \,\mathrm{d}V\tag{1} \end{align} [/math] [math] \begin{align} {\oint}\!\!\!\!{\oint}_{\scriptstyle \partial \Omega } & \mathbf{B}\cdot\mathrm{d}\mathbf{S} = 4 \pi \iiint_\Omega \rho_m \,\mathrm{d}V\tag{2} \end{align} [/math] [math] \begin{align} - \oint_{\partial \Sigma} & \mathbf{E} \cdot \mathrm{d}\boldsymbol{l} = \frac{1}{c} \left(\frac{\mathrm{d}}{\mathrm{d}t} \iint_{\Sigma} \mathbf{B} \cdot \mathrm{d}\mathbf{S} + 4 \pi \iint_{\Sigma} \mathbf{J_m} \cdot \mathrm{d}\mathbf{S} \right) \tag{3}\\ \end{align} [/math] [math] \begin{align} \oint_{\partial \Sigma} & \mathbf{B} \cdot \mathrm{d}\boldsymbol{l} = \frac{1}{c} \left(\frac{\mathrm{d}}{\mathrm{d}t} \iint_{\Sigma} \mathbf{E} \cdot \mathrm{d}\mathbf{S} + 4 \pi \iint_{\Sigma} \mathbf{J_e} \cdot \mathrm{d}\mathbf{S} \right) \tag{4}\\ \end{align} [/math] A few words first on the meanings of the integral symbols... The number of integral signs indicates whether you're integrating over one, two or three dimensions. To calculate the treble integral in equation (1) you might integrate first on [math]x[/math], then on [math]y[/math], then on [math]z[/math]. The integral doesn't have to be calculated that way. You can get the volume integral perfectly well in other ways. For example, if the volume you are integrating over is spherical, one of your integrations might be over a radial distance. The subscript to the integrals, such as [math]\Omega[/math] is giving a name to the volume you are integrating over, so you can describe its shape elsewhere. The [math]\scriptstyle \partial \Omega[/math] subscript on the integral is representing the surface of the volume [math]\Omega[/math]. In these equations, [math]\Sigma[/math] is a convenient Greek letter name to give to a surface. These equations are not using the common convention that [math]\Sigma[/math] means 'a sum'. The [math]\scriptstyle \partial \Sigma[/math] subscript on the integral is representing the edge of a, typically disk shaped, surface [math]\Sigma[/math]. The circular symbol superimposed over the middle of an integral is a hint that the line or area being integrated over is a loop in the case of a line, or a closed surface like the surface of a sphere in the case of an area. In equation (1) you consider any volume of space, [math]\Omega[/math]. The right hand side is integrating all charge [math]\rho_e[/math] in that volume. [math]\scriptstyle \partial \Omega[/math] represents the surface of that volume. The left hand side is a surface integral, over the surface of [math]\Omega[/math], integrating electric field. The dot product with [math]E[/math] inside the integral ensures it is measuring how much electric field crosses the surface. Equation (2) is the same thing for magnetic field and 'magnetic charge'. As [math]\rho_m[/math] is zero everywhere, the right hand side evaluates to zero. In equation (4) you consider a 'loop' in space that is the edge of some surface [math]\Sigma[/math]. [math]\scriptstyle \partial \Sigma[/math] is the edge of the surface [math]\Sigma[/math]. The left hand side with its dot product is measuring the magnetic field around the loop. The right hand side is measuring the change in electric field through the surface, and adding in the electric current through the surface (electric current density integrated over the surface [math]\Sigma[/math]). Equation (3) does the same thing for electric field around the loop and magnetic field crossing the surface, and as [math]J_m = 0[/math] the 'magnetic current' term disappears.

Using Complex Numbers

Rather than treating magnetic field and electric field as separate things, you can combine them, using complex numbers.

Four Equations to two - Using [math]\mathbb{C}[/math]omplex numbers

Put: [math]\begin{align} \mathbf{F} = \mathbf{B} + i\mathbf{E} \end{align}[/math] Then [math]\mathbf{F}[/math] has combined electromagnetic and magnetic fields into one complex valued vector field that represents both. Do the same thing for [math]\rho[/math] and [math]\mathbf{J}[/math], i.e. [math]\rho=\rho_m + i\rho_e[/math] and [math]\mathbf{J}=\mathbf{J}_m+i\mathbf{J}_e[/math] and the four equations now reduce down to two: [math]\begin{align} \nabla \cdot \mathbf{F} = 4\pi\rho \end{align}[/math] [math]\begin{align} \nabla \times \mathbf{F} = \frac{i}{c}\left( \frac{\partial \mathbf{F}}{\partial t} + 4\pi\mathbf{J} \right)\end{align}[/math] An important detail is how the minus sign has been absorbed into the multiplications by [math]i[/math]. In the original equations the second derivative of [math]\mathbf{B}[/math] (or indeed of [math]\mathbf{E}[/math]) appears from combining both equations (3) and then (4), and is related to the original with a minus sign, picked up from equation (3). Now instead one picks up two multiplications by [math]i[/math]. It's the same thing, but done more symmetrically. In one sense this reformulation in terms of complex numbers does not simplify anything. The four equations in real values are still there 'behind' the two equations in complex values. In a different sense it has done something worthwhile. It has brought out that magnetic and electromagnetic fields are two aspects of the same field.

To Dig Deeper

To dig deeper: Caches-to-Caches - A nuanced description of Maxwell's equations that aim to make the physics more understandable. The use of the more symmetric version of the equations is inspired by that article.

To dig deeper: Wikipedia - As ever Wikipedia aims to be encyclopedic, making the subject matter more than a bit impenetrable.