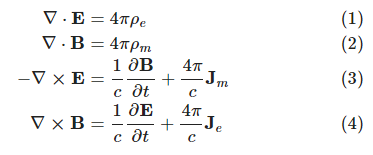Maxwell's equations

Maxwell's equations are partial differential equations that state the relationships between electric and magnetic fields. They underlie the wave nature of light. Equation (1) and (2) are Gauss' laws, (3) Faraday's law, (4) Ampere's.

The four equations were originally formulated based on observation. Equation 3, for example, comes from Faraday's law. It relates the rate at which magnetic field is changing, [math]\frac{\partial\mathbf{B}}{\partial t}[/math] to circular flow of electric current, [math]\nabla\boldsymbol{\times}\mathbf{E}[/math].

Maxwell's genius was in completing the four equations, bringing them together, and from the combination conjecturing that light and radio waves were electromagnetic phenomenon. In particular, the speed at which light travels can be deduced from the equations.

Prerequisities

The maths of these equations will make no sense to you whatsoever without the following foundations:

• Understanding of Simple harmonic motion. The key idea is that differential equations relating position, velocity and acceleration can lead to a solution that oscillates.
• Familiarity with vectors in 3 dimensions, Vector product and Cross product. The mathematical operations allow you to calculate the angle between vectors or to take two vectors and find another that is perpendicular to both.
• The Div Grad and Curl differential operations in 3D that are shown here, and in particular why [math]\nabla\cdot(\nabla\times\mathbf{B}) = 0[/math]. Div, Grad and Curl are differential operations in 3D space. Maxwell's 3rd and 4th equation relate the results of a spatial derivative of one field (magnetic or electric) with a temporal derivative of the other kind of field.

No Magnetic Monopoles

To-Be-Written.

Integral Version

The four differential equations are equivalent to these four integral equations. If you differentiate these integral equations, you get the differential ones.

[math] \begin{align} \oint_{\scriptstyle\partial \Omega } & \mathbf{E}\cdot\mathrm{d}\mathbf{S} = 4 \pi \iiint_\Omega \rho_e \,\mathrm{d}V\tag{1} \end{align} [/math]

[math] \begin{align} \oint_{\scriptstyle \partial \Omega } & \mathbf{B}\cdot\mathrm{d}\mathbf{S} = 4 \pi \iiint_\Omega \rho_m \,\mathrm{d}V\tag{2} \end{align} [/math]

[math] \begin{align} - \oint_{\partial \Sigma} & \mathbf{E} \cdot \mathrm{d}\boldsymbol{l} = \frac{1}{c} \left(\frac{\mathrm{d}}{\mathrm{d}t} \iint_{\Sigma} \mathbf{B} \cdot \mathrm{d}\mathbf{S} + 4 \pi \iint_{\Sigma} \mathbf{J_m} \cdot \mathrm{d}\mathbf{S} \right) \tag{3}\\ \end{align} [/math]

[math] \begin{align} \oint_{\partial \Sigma} & \mathbf{B} \cdot \mathrm{d}\boldsymbol{l} = \frac{1}{c} \left(\frac{\mathrm{d}}{\mathrm{d}t} \iint_{\Sigma} \mathbf{E} \cdot \mathrm{d}\mathbf{S} + 4 \pi \iint_{\Sigma} \mathbf{J_e} \cdot \mathrm{d}\mathbf{S} \right) \tag{4}\\ \end{align} [/math]

To Dig Deeper

To dig deeper: Maxwell's equations - A nuanced description of Maxwell's equations that aim to make the physics more understandable. The use of the more symmetric version of the equationsTemplate:Cite is inspired by that article.

To dig deeper: Wikipedia - As ever Wikipedia aims to be encyclopedic, making understanding the subject matter more than a bit impenetrable.